ज्यामितीय आकृति: त्रिभुज

इस प्रकाशन में, हम मुख्य ज्यामितीय आकृतियों में से एक - एक त्रिभुज की परिभाषा, वर्गीकरण और गुणों पर विचार करेंगे। हम प्रस्तुत सामग्री को समेकित करने के लिए समस्याओं को हल करने के उदाहरणों का भी विश्लेषण करेंगे।

त्रिभुज की परिभाषा

त्रिकोण - यह एक समतल पर एक ज्यामितीय आकृति है, जिसमें तीन भुजाएँ होती हैं, जो तीन बिंदुओं को जोड़कर बनती हैं जो एक सीधी रेखा पर नहीं होती हैं। पदनाम के लिए एक विशेष प्रतीक का उपयोग किया जाता है - ।

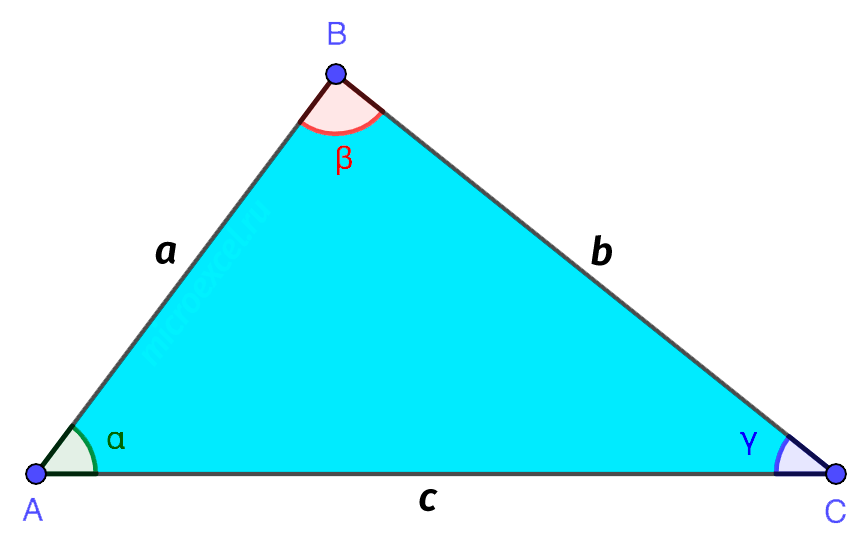
• बिंदु A, B और C त्रिभुज के शीर्ष हैं।
• खंड AB, BC और AC त्रिभुज की भुजाएँ हैं, जिन्हें अक्सर एक लैटिन अक्षर के रूप में दर्शाया जाता है। उदाहरण के लिए, एबी = a, ईसा पूर्व = b, और = c.
• त्रिभुज का आंतरिक भाग त्रिभुज की भुजाओं से घिरा तल का वह भाग होता है।

शीर्ष पर त्रिभुज की भुजाएँ तीन कोण बनाती हैं, जिन्हें पारंपरिक रूप से ग्रीक अक्षरों से दर्शाया जाता है - α, β, γ आदि इसी कारण त्रिभुज को तीन कोनों वाला बहुभुज भी कहते हैं।

कोणों को विशेष चिन्ह का उपयोग करके भी दर्शाया जा सकता है "∠"

• α - BAC या CAB
• β - ABC या CBA
• γ - ACB या BCA

त्रिभुज वर्गीकरण

कोणों के आकार या समान भुजाओं की संख्या के आधार पर, निम्न प्रकार की आकृतियों को प्रतिष्ठित किया जाता है:

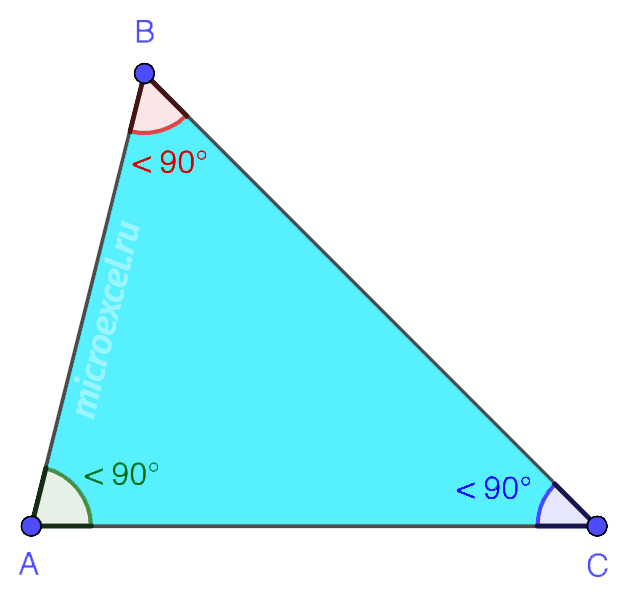
1. तीव्र कोण - एक त्रिभुज जिसमें तीनों कोण न्यून हों, यानी 90° से कम।

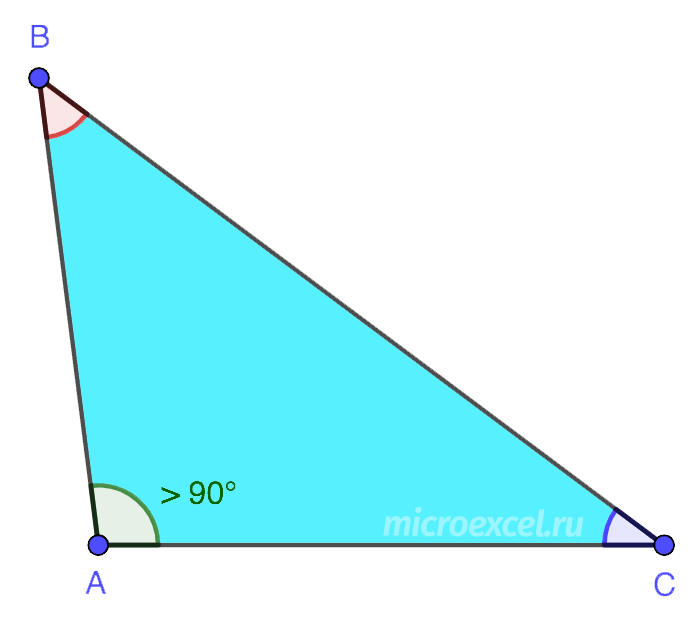
2. कुंठित एक त्रिभुज जिसमें एक कोण 90° से बड़ा होता है। अन्य दो कोण न्यून हैं।

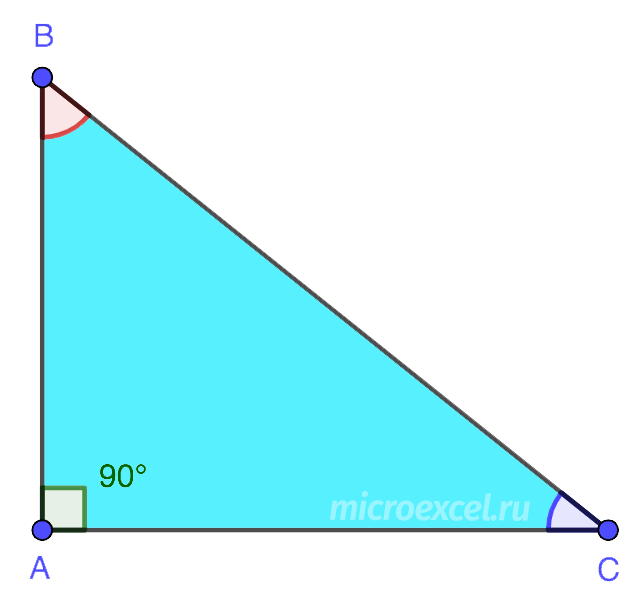
3. आयताकार - ऐसा त्रिभुज जिसमें एक कोण समकोण हो, अर्थात 90° के बराबर हो। ऐसी आकृति में, दो भुजाएँ जो एक समकोण बनाती हैं, टाँगें (AB और AC) कहलाती हैं। समकोण के विपरीत तीसरी भुजा कर्ण (BC) है।

4. बहुमुखी एक त्रिभुज जिसमें सभी भुजाओं की लंबाई अलग-अलग होती है।

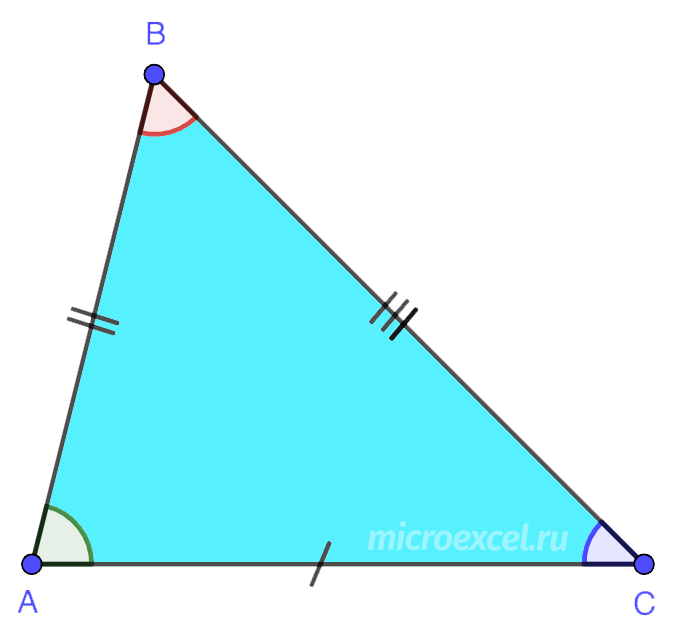
5. समद्विबाहु - एक त्रिभुज जिसकी दो बराबर भुजाएँ होती हैं, जिन्हें पार्श्व (AB और BC) कहते हैं। तीसरा पक्ष आधार (एसी) है। इस आकृति में, आधार कोण बराबर हैं (∠BAC = ∠BCA)।

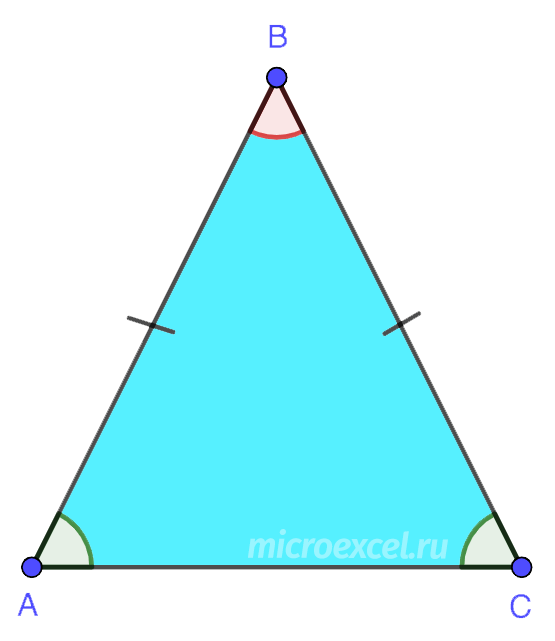
6. समबाहु (या सही) एक त्रिभुज जिसकी सभी भुजाएँ समान लंबाई की हों। साथ ही इसके सभी कोण 60° के होते हैं।

त्रिभुज गुण

1. त्रिभुज की कोई भी भुजा अन्य दो से छोटी है, लेकिन उनके अंतर से बड़ी है। सुविधा के लिए, हम पक्षों के मानक पदनाम स्वीकार करते हैं - a, b и с… फिर:

बी - सी <ए <बी + सीAt बी> सी

इस गुण का उपयोग रेखा खंडों का परीक्षण करने के लिए किया जाता है यह देखने के लिए कि क्या वे एक त्रिभुज बना सकते हैं।

2. किसी भी त्रिभुज के कोणों का योग 180° होता है। इस गुण से यह निष्कर्ष निकलता है कि एक अधिक त्रिभुज में दो कोण सदैव न्यून होते हैं।

3. किसी भी त्रिभुज में, बड़ी भुजा के सम्मुख एक बड़ा कोण होता है, और इसके विपरीत।

कार्यों के उदाहरण

टास्क 1

त्रिभुज में दो ज्ञात कोण होते हैं, 32° और 56°। तीसरे कोण का मान ज्ञात कीजिए।

उपाय

आइए ज्ञात कोणों को के रूप में लें α (32 डिग्री) और β (56°), और अज्ञात - पीछे γ.

सभी कोणों के योग के गुण के अनुसार, ए + बी + सी = 180 डिग्री।

नतीजतन, γ = 180 डिग्री - ए - बी = 180 ° - 32 ° - 56 ° = 92 °।

टास्क 2

लंबाई 4, 8 और 11 के तीन खंड दिए गए हैं। पता करें कि क्या वे एक त्रिभुज बना सकते हैं।

उपाय

आइए हम ऊपर चर्चा की गई संपत्ति के आधार पर दिए गए प्रत्येक खंड के लिए असमानताओं की रचना करें:

11 - 4 <8 <11 + 4
8 - 4 <11 <8 + 4
11 - 8 <4 <11 + 8

ये सभी सही हैं, इसलिए ये खंड एक त्रिभुज की भुजाएँ हो सकते हैं।